I was playing with some numbers on challenges we can face when it comes communicating within a chain of people. I remember playing the telephone game as a child, and was amazed at how what was told to the first participant was rarely what was repeated by the last. Sometimes, similar communication challenges can be observed in a professional environment.
What does that look like on paper? Let’s say person A is speaking with person B. In the interaction (speaking and listening), there is a chance of accidental miscommunication. For my back of the envelope calculation, I assumed that the chance of miscommunication is constant in an interaction between any two people on the same topic. So, if we assume that one out of ten times there is a miscommunication in an interaction I could look at it like this:
Of course, any of the interactions has a 1/10 chance of miscommunication. It doesn’t have to be the 10th one. It could also happen like this.

Mathematically, we can create a table summarizing the chance the last recipient receives miscommunication. If there is a 1/10 chance of miscommunication, then in one interaction there is a 1/10 chance of miscommunication – or put another way a 9/10 chance of no miscommunication. If there are three people, there are two interactions. There is a 9/10 * 9/10 = 0.81 chance of there being no miscommunication, where we can get the chance of miscommunication by calculating 1- (1/10 * 1/10) = 0.19. Following this logic we can create a table of the probability of miscommunication based on the size of the group playing the proverbial game of telephone.

Or, to put it graphically:
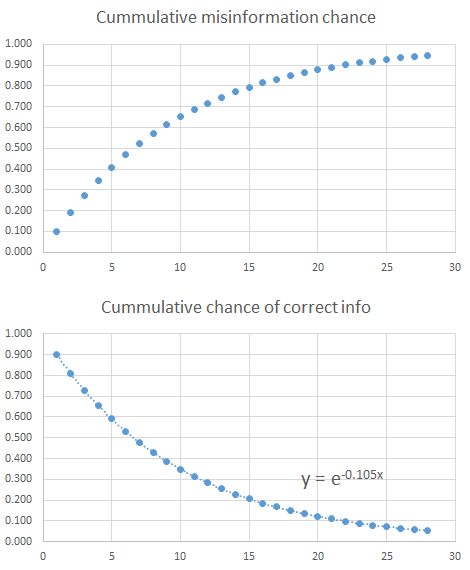
Of course, the 1/10 is completely made up. However, this does demonstrate how important it is to consider group size when communicating. If you are hearing something from someone who heard it from someone who heard if from someone, be skeptical. And, when trying to communicate something important, one on one communication may be better than the grapevine.